Dependency resolving algorithm

Thursday, August 7th, 2008

Here’s a little explanation of a possible dependency resolution algorithm. I’ve made this as basic as possible, so it’s easy to understand. If you’re at home in (graph) algorithms, this post is probably not of much interest to you.

Premise

Suppose we have five objects which all depend on some of the other objects. The objects could be anything, but in this case let’s say they’re very simple software packages (no minimal versions, etc) that depend on other packages which must be installed first. How does one find the right order of installing the packages?

Take, for instance, the following scenario: Software package ‘a’ depends on ‘b’ and ‘d’. ‘b’ depends on ‘c’ and ‘e’. ‘c’ depends on ‘d’ and ‘e’. ‘d’ depends on nothing, nor does ‘e’. When we visualize this, we get something like this:

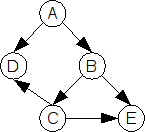
Representing the data: Graphs

In order to find the correct sequence of installing the software packages, we must first represent the data in our program. This is where graphs come into the picture. A graph is a simple data structure that consists of nodes (sometimes called vertices) and edges. In our case, each software package is a node. Nodes are connected to each other by something called ‘edges’. In our case, an edge from one node to another signifies that the first node is dependent on the second. This relationship ‘depends’ is implicit in our program, since all we’re doing is resolving dependencies. But edges can represent any other kind of relationship between nodes, such as ‘has a road to’ or ‘knows’ (if your nodes as persons), etc.

Lets define a class that can hold our node information. We’ll need to store the name of the node, and a list of relationships (dependencies) to other nodes. We’re using the Python language for this, by the way. For those that don’t know Python: don’t worry. I’ll try to explain things as we go along. This is what our Node class will look like:

class Node:
   def __init__(self, name):
      self.name = name
      self.edges = []

   def addEdge(self, node):
      self.edges.append(node)

This is a class which can hold a name and a list (array) of edges. ‘[]’ in Python denotes a new empty list/array. We also have a method for adding edges to the node, which takes a node and adds it to the list of nodes which this node is dependent on.

Now, let’s define our test data. First, we create a bunch of nodes:

a = Node('a')
b = Node('b')
c = Node('c')
d = Node('d')
e = Node('e')

Next, we define the relationships between our nodes:

a.addEdge(b)    # a depends on b
a.addEdge(d)    # a depends on d
b.addEdge(c)    # b depends on c
b.addEdge(e)    # b depends on e
c.addEdge(d)    # c depends on d
c.addEdge(e)    # c depends on e

Algorithm: Walking the graph

Okay, we’ve got our data defined now. Now comes the somewhat harder part of the dependency resolving: the algorithm. Let’s just take it one step at a time by not concerning ourselves with any actual depency resolution or any of the other problems we’ll run into.

We’ll start with walking through the graph. For this, we need a starting point, which will be node ‘a’. We start at ‘a’, and then we have to go through all the nodes that are connected to ‘a’. For each of those connected nodes, we have to go through that node’s connected nodes, etc. So we write a recursive function that calls itself for each node connected to the current node:

def dep_resolve(node):
   print node.name
   for edge in node.edges:
      dep_resolve(edge)

dep_resolve(a)

The output of which is:

a
b
c
d
e
e
d

Algorithm: Dependency resolution order

Now we need to determine the resolution order of our dependencies. When can a piece of software be installed? Software ‘a’ depends on ‘b’ and ‘d’, so ‘a’ can’t be installed yet. ‘d’, however, doesn’t depend on anything, so it can be installed. A software package can be installed when all of its dependencies have been installed, or when it doesn’t have any dependencies at all. When we look at our recursive function above, we see that the point at which all dependencies for the current node have been installed (resolved) is right after we’ve gone through all the edges (dependencies) of the current node. When we reach that point, we append the current node to a list (array) of resolved dependencies. Our function now looks like this:

def dep_resolve(node, resolved):
   print node.name
   for edge in node.edges:
      dep_resolve(edge, resolved)
   resolved.append(node)

It now takes two arguments: node and resolved, which is the list (array) of resolved nodes. Lists in Python are objects, so they are always passed by reference. So when one of the iterations of the recursive function adds a node to the list, that change is reflected in all the iterations.

We call the function, and output the result:

resolved = []
dep_resolve(a, resolved)
for node in resolved:
   print node.name, 

Output is:

a
b
c
d
e
e
d
d e c e b d a

Algorithm: Already resolved nodes

The last line shows the contents of the resolved list. As you can see, some nodes appear twice. This is because sometimes more than one software package depends on the same package. But we only need to install each package once. We can eliminate that rather easily. When a package has already been resolved, we don’t need to visit it again. We add this logic to our function by first checking the resolved list to see if the node we’re about to visit is already in it:

def dep_resolve(node, resolved):
   print node.name
   for edge in node.edges:
      if edge not in resolved:
         dep_resolve(edge, resolved)
   resolved.append(node)

When we now run the program, the output is:

a
b
c
d
e
d e c b a

That’s better. We now have our dependency resolution! ‘d’ needs to be installed first, then ‘e’, then ‘c’, etc.

Algorithm: Detecting circular dependencies

But, we’ve got a problem. Suppose we add the following to our dependencies:

d.addEdge(b)

This makes the graph look like this:

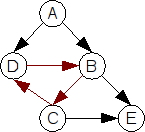
Node ‘d’ now depends on ‘b’. But ‘b’ depends on ‘c’ and ‘c’ depends on ‘d’ and ‘d’ depends on ‘b’ and… We’ve now got a circular dependency which can never be solved. When we run the program, this becomes evident:

[long repetition of stack traces]
  File "./foo.py", line 47, in dep_resolve
    dep_resolve(edge, resolved)
  File "./foo.py", line 47, in dep_resolve
    dep_resolve(edge, resolved)
  File "./foo.py", line 47, in dep_resolve
    dep_resolve(edge, resolved)
RuntimeError: maximum recursion depth exceeded

We’ll never be able to reliably determine whether ‘d’ or ‘b’ should be installed first, because they both (indirectly) depend on each other. This is a logic error in our dependencies, and there is nothing our algorithm can do about it. But we CAN detect it, and signal the user about the problem. When does a circular dependency occur? When we think about that for a moment, we can determine that: a circular dependency is occurring when we see a software package more than once, unless that software package has all its dependencies resolved.. We’ve already built in logic for skipping nodes that have already been satisfied (have all their dependencies resolved), so all we need to do is check if a node has already been seen before. Let’s implement that in our function:

def dep_resolve(node, resolved, seen):
   print node.name
   seen.append(node)
   for edge in node.edges:
      if edge not in resolved:
         if edge in seen:
            raise Exception('Circular reference detected: %s -> %s' % (node.name, edge.name))
         dep_resolve(edge, resolved, seen)
   resolved.append(node)

We’ve added a ‘seen’ argument to the function’s signature. This is largely the same as the ‘resolved’ argument, except that it holds all the seen nodes. After checking if the node has already been resolved, we’ve added logic to check that the node hasn’t been seen before. If it has been seen before, we raise an exception which stops our algorithm.

We now run this like so:

resolved = []
dep_resolve(a, resolved, [])
for node in resolved:
   print node.name,

We pass an empty list for the ‘seen’ argument, since we don’t care about its contents after our function is done. The output:

a
b
c
d
Traceback (most recent call last):
  File "./foo.py", line 66, in <module>
    dep_resolve(a, resolved, [])
  File "./foo.py", line 62, in dep_resolve

    dep_resolve(edge, resolved, seen)
  File "./foo.py", line 62, in dep_resolve
    dep_resolve(edge, resolved, seen)
  File "./foo.py", line 62, in dep_resolve
    dep_resolve(edge, resolved, seen)
  File "./foo.py", line 61, in dep_resolve
    raise Exception('Circular reference detected: %s -> %s' % (node.name, edge.name))
Exception: Circular reference detected: d -> b

Algorithm: Optimization

We’re keeping a list of all the nodes we’ve seen in the program above. But we’ve previously determined that a circular reference is occuring when we see a software package more than once, unless that software package has all its dependencies resolved. This means we don’t need to remember the nodes we’ve seen if they are already resolved. This can save us some memory and processing time, since we only have to check a maximum of ‘n’ (where ‘n’ is the number of nodes in the graph) times each iteration. The way to go about this is to simply remove the node from the seen list once it has been resolved. We also rename our ‘seen’ list to ‘unresolved’ since that better describes what it does now:

def dep_resolve(node, resolved, unresolved):
   unresolved.append(node)
   for edge in node.edges:
      if edge not in resolved:
         if edge in unresolved:
            raise Exception('Circular reference detected: %s -> %s' % (node.name, edge.name))
         dep_resolve(edge, resolved, unresolved)
   resolved.append(node)
   unresolved.remove(node)

Conclusion and some tips

That’s it! Our algorithm is done. I’ve taken you step by step through writing a dependency resolving algorithm. Of course, this one was rather easy, and in order to make it as clear as possible, I followed an iterative explanation of how to write the algorithm. In real life, when writing algorithms, you’d do best by first thinking about the rules of the algorithm before starting on an implementation. When writing algorithms, it’s often easy to get confused because of implementation specifics. I’ve found two things help immensely when writing algorithms:

• Visualize
  It helps to visualize the data as it goes through the algorithm. When designing the algorithm, make drawings. When implementing the algorithm try to represent the data in a clear way through each step of the algorithm.
• Think about rules, not implementation details
  Don’t think about algorithms in a computer-language mindset. Upfront, try to determine which rules the system must adhere by. Thinking about implementation details often confuses your reasoning. Don’t think about recursive function calling for instance, but think about software packages that need to be installed.

I will usually determine the rules of the system up front. In this case, the rules where:

1. A software package can be installed when all of its dependencies have been installed, or when it doesn’t have any dependencies at all.
2. When a package has already been resolved, we don’t need to visit it again.
3. A circular dependency is occurring when we see a software package more than once, unless that software package has all its dependencies resolved.

The algorithm described in this post is rather naive. I’m sure there are many ways in which it can be optimized. I haven’t looked into completely different strategies in which this problem can be solved, but I’m sure there are better ones. This one, however, is rather simple to understand and implement, and scales pretty well in most situations.

Update June 2, 2013: David Kaye has written a Javascript version based on this algorithm.